沒有成本的遍歷(travesal)、展開樹:
DFS(深度優先):
DFS是使用到遞迴的演算法,將圖中的點都經過一次。
DFS的複雜度:
時間複雜度:O(|V|+E)
空間複雜度:O(V)
DFS的應用:
1.找到一段路徑
2.測試此圖是否為二分圖
3.測試是否為強連通性
4.偵測是否有Cycle
DFS的pseudo code
1.走訪u點
2.偵測鄰近u的點,設此點為v
3.走訪v點
4.重複3、4直到所有的點都被走訪或已無可以走訪的點
DFS(G, u)
u.visited = true
for each v ∈ G.Adj[u]
if v.visited == false
DFS(G,v)
init() {
For each u ∈ G
u.visited = false
For each u ∈ G
DFS(G, u)
}BFS(廣度優先):
BFS又可稱為level order travesal
BFS的複雜度:
時間複雜度:O(|V|+E)
空間複雜度:O(V)
BFS的應用:
1.GPS導航
2.偵測在無向圖中是否有cycle
3.最小成本展開樹
BFS的pseudo code
0.準備一個queue 和 visited list
1.將第一個走訪的點u放入queue
2.將queue的第一筆u放入visited list
3.將u相鄰且未被拜訪的點放入queue
4.重複2.3.直到所有的點都被拜訪
create a queue Q
mark v as visited and put v into Q
while Q is non-empty
remove the head u of Q
mark and enqueue all (unvisited) neighbours of u有成本的遍歷,找出最小成本展開樹
Kruskal
1.greedy
Kruskal的複雜度:
時間複雜度:O(E log E)
Kruskal的pseudo code
1.將邊的權重從小排到大排序好
2.依序加入權重最低的邊,如果加入後會產生cycle則放棄
3.直到所有的點都被走訪過
KRUSKAL(G):
A = ∅
For each vertex v ∈ G.V:
MAKE-SET(v)
For each edge (u, v) ∈ G.E ordered by increasing order by weight(u, v):
if FIND-SET(u) ≠ FIND-SET(v):
A = A ∪ {(u, v)}
UNION(u, v)
return Aprim
Prim 的算法不是從邊開始,而是從頂點開始,並不斷添加不在樹中的最低權重邊,直到所有頂點都被覆蓋。
greedy
prim的複雜度:
時間複雜度:O(E logV)
prim的應用:
- 鋪設電線電纜
- 在網絡設計
- 在網絡週期中製定協議
prim的pseudo code
1.從點V開始
2.找到和其他未被訪問的點,且選中其中最小權重的邊
3.重複2.直到完成MST
T = ∅;
U = { 1 };
while (U ≠ V)
let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U;
T = T ∪ {(u, v)}
U = U ∪ {v}找出某個點到其他點的最短距離
Dijkstra
1.與最小成本展開樹不同的是,點與點之間最短的路徑可能不一定包括所有的點。
2.使用greedy algo.
Dijkstra的複雜度:
時間複雜度:O(E logV)
空間複雜度:O(V)
Dijkstra的應用
1.在社交網絡應用中
2.在地圖中找位置
Dijkstra的pseudo code
function dijkstra(G, S)
for each vertex V in G
distance[V] <- infinite
previous[V] <- NULL
If V != S, add V to Priority Queue Q
distance[S] <- 0
while Q IS NOT EMPTY
U <- Extract MIN from Q
for each unvisited neighbour V of U
tempDistance <- distance[U] + edge_weight(U, V)
if tempDistance < distance[V]
distance[V] <- tempDistance
previous[V] <- U
return distance[], previous[]Bellman Ford
類似於dijkstra,但可以有負邊,不過還是不可以有負cycle。
透過greedy找最小邊
Bellman Ford的複雜度:
時間複雜度:
- 最好O(E)
- 平均O(VE)
- 最差O(VE)
空間複雜度:O(V)
Bellman Ford的pseudo code
function bellmanFord(G, S)
for each vertex V in G
distance[V] <- infinite
previous[V] <- NULL
distance[S] <- 0
for each vertex V in G
for each edge (U,V) in G
tempDistance <- distance[U] + edge_weight(U, V)
if tempDistance < distance[V]
distance[V] <- tempDistance
previous[V] <- U
for each edge (U,V) in G
If distance[U] + edge_weight(U, V) < distance[V}
Error: Negative Cycle Exists
return distance[], previous[]找到所有點到所有點的最短距離:
Floyd-Warshell
1.為dynamic programing
2.適用於有向和無向加權圖。但是,它不適用於具有負循環的圖
Floyd-Warshell的複雜度:
時間複雜度:O(n3)
空間複雜度:O(n2)
Floyd-Warshell的應用:
- 求最短路徑是有向圖
- 找到有向圖的傳遞閉包
- 求實矩陣的求逆
- 用於測試無向圖是否是二分圖
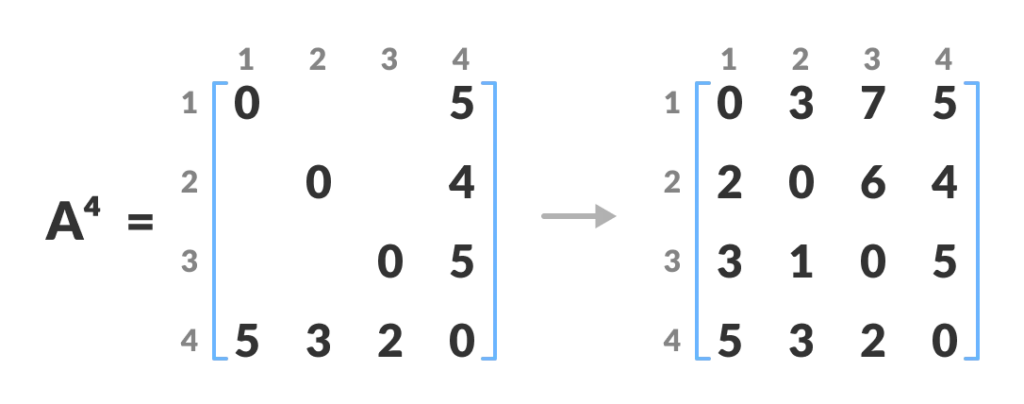
Floyd-Warshell的過程:
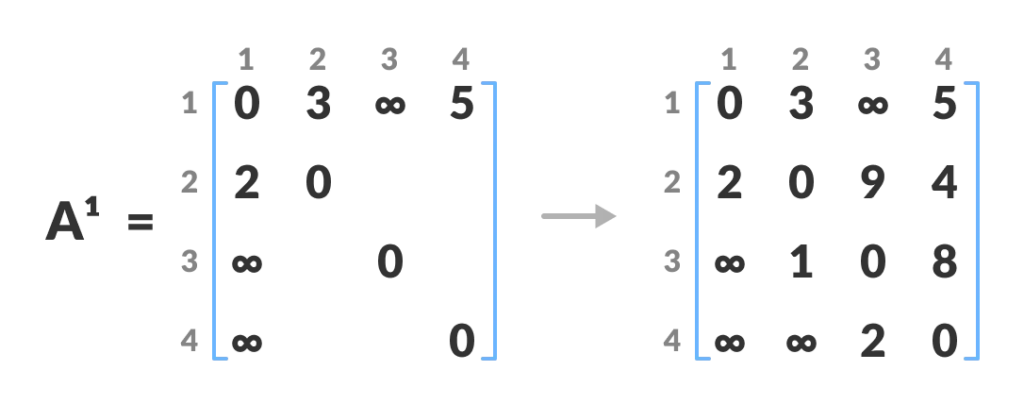
1.建立A0:成本矩陣
2.建立A1,代表k=1,k代表此次可以經過的中間節點,如果經過了中間節點後的權重<沒有經過,則取代。
- 數學式:A[i][j]=(A[i][k] + A[k][j]) if (A[i][j] > A[i][k] + A[k][j])
如圖:
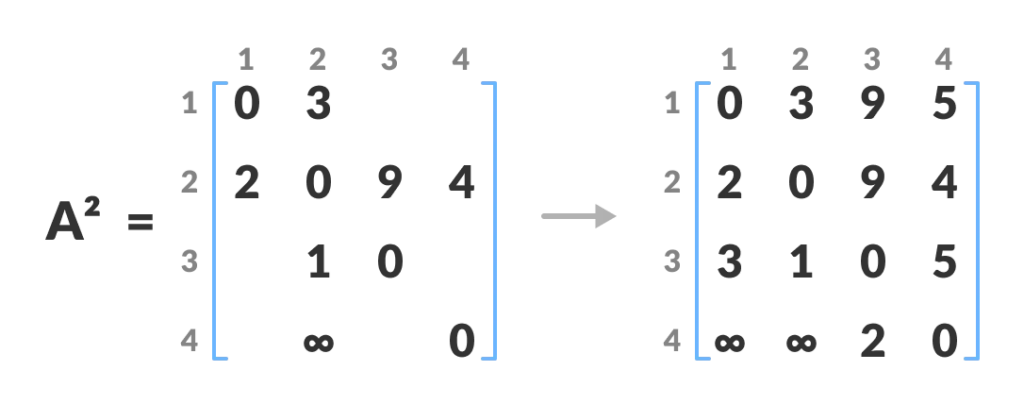
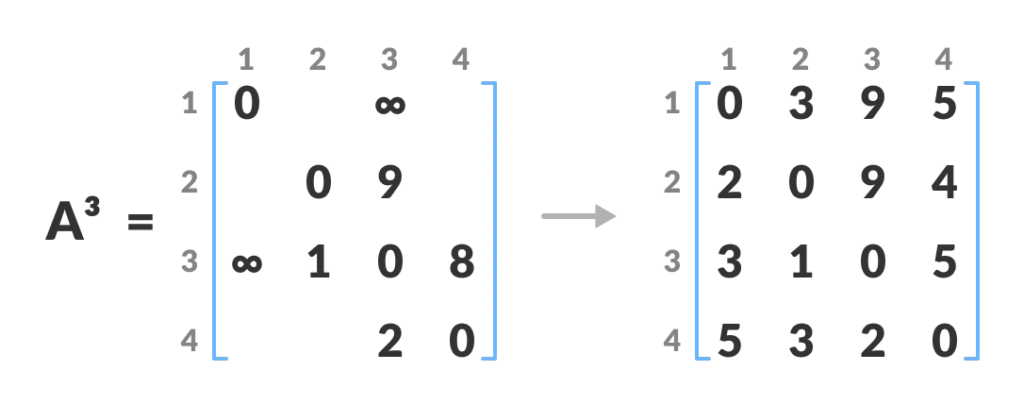
3.建立A2.....,直到k=4(此圖vertex=4)
Floyd-Warshell的pseudo code
n = no of vertices
A = matrix of dimension n*n
for k = 1 to n
for i = 1 to n
for j = 1 to n
Ak[i, j] = min (Ak-1[i, j], Ak-1[i, k] + Ak-1[k, j])
return A